Coordinates and projections

How do we match feature data to the Earth?

• In the last section, we noted that vector data is like a game of connect the dots
• But how do we tell a computer where the dots are?
• Each dot is a coordinate in space, with x and y positions (and sometimes z if we're including elevation)
• There are thousands of different coordinate reference systems that are used to match points to the Earth's surface

If you go to Google Maps and right click anywhere on the map, the first entry in the menu will be the WGS 84 coordinates of the place you just clicked.

• The most common is known as WGS 84, and it uses latitude and longitude.
  • In WGS 84, the coordinate (0, 0) is at the intersection of the Equator and the Prime Meridian in the Gulf of Guinea
  • The front door of the Boston Public Library is (42.34953, -71.0775). The first number is positive because we're north of the Equator, and the second is negative because we're west of the Prime Meridian
  • Try copying these coordinates into Google Maps—see where you land!
• There are many other coordinate systems that are used for different purposes

TIP

Confusing coordinate systems are one of the number one reasons why you might encounter problems with data! While many modern data sets are standardizing on WGS 84 coordinates, you'll want to figure out what coordinate system your data is in when you access it. You can either find the coordinate system on the portal you downloaded the data from or by bringing it into GIS software.

Map projections

Consider this: Can you think of how ways in which projections relate to power and representation? Why might certain countries or people prefer one projection to another?

• If we ask the computer to graph the coordinates directly onto the screen, that's called an unprojected presentation.
• However, oftentimes we'll want to choose a projection which transforms the source coordinates into rendered coordinates on the screen or page.
• Projections allow us to see the Earth's surface, which is curved, in two dimensions.
• At smaller scales, like a single neighborhood, the projection doesn't make a huge difference, because there's not a lot of curvature in a small space.
• But at the global scale, a projection makes a huge difference in what we see, because the projection controls how the round Earth is made into a flat representation.

Example: Goode Homolosine projection

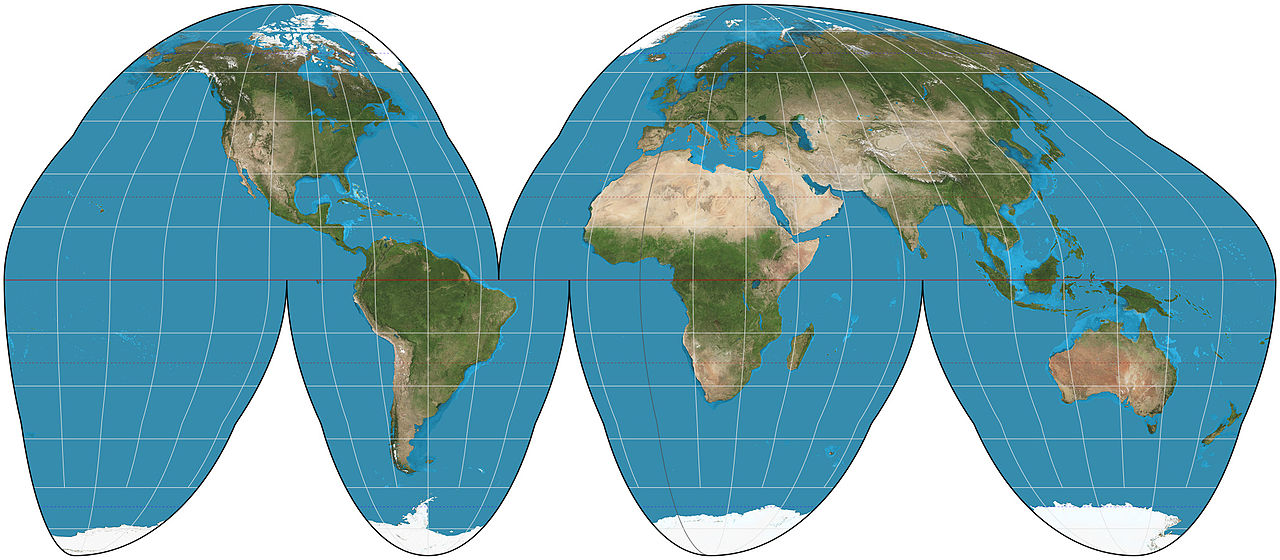
Goode Homolosine projection, Strebe, Wikipedia.

Example: Mercator projection

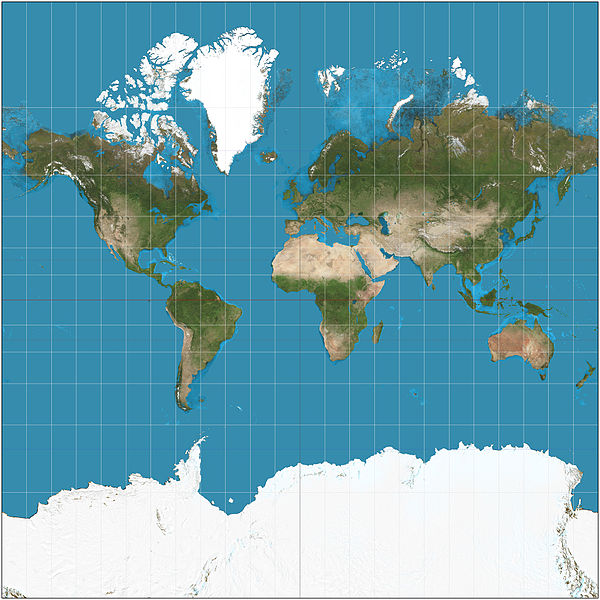
Mercator Projection, Strebe, Wikipedia.

• Projections can intentionally or unintentionally perpetuate pre-existing power structures and even construct new ones.

More reading on why projections matter

Comprehension check

How many different numbers are necessary, at a minimum, to define a coordinate?

1

2

3

Which of these two maps will be more distorted depending on which projection system is chosen?

A map of Copley Square

A map of North America